Minggu, 17 April 2011

Persamaan Linear & Matriks

Persamaan linear dapat dinyatakan sebagai matriks. Misalnya persamaan:
3x1 + 4x2 − 2 x3 = 5
x1 − 5x2 + 2x3 = 7
2x1 + x2 − 3x3 = 9
dapat dinyatakan dalam matriks teraugmentasi sebagai berikut
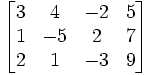
\begin{bmatrix} 3 & 4 & -2 & 5\\ 1 & -5 & 2 & 7\\ 2 & 1 & -3 & 9\\ \end{bmatrix}
Penyelesaian persamaan linier dalam bentuk matriks dapat dilakukan melalui beberapa cara, yaitu dengan eliminasi Gauss atau dapat juga dengan cara eliminasi Gauss-Jordan. Namun, suatu sistem persamaan linier dapat diselesaikan dengan eliminasi Gauss untuk mengubah bentuk matriks teraugmentasi ke dalam bentuk eselon-baris tanpa menyederhanakannya. Cara ini disebut dengan substitusi balik.
Sebuah sisitem persamaan linier dapat dikatakan homogen apabila mempunyai bentuk :
a11x1 + a12x2 + ... + a1nxn = 0
a21x1 + a22x2 + ... + a2nxn = 0
am1x1 + am2x2 + ... + amnxn = 0
Setiap sistem persamaan linier yang homogen bersifat adalah tetap apabila semua sistem mepunyai x1 = 0 , x2 = 0 , ... , xn = 0 sebagai penyelesaian. Penyelesaian ini disebut solusi trivial. Apabila mempunyai penyelesaian yang lain maka disebut solusi nontrivial.

Penyelesaian Persamaan Linear dengan Matriks

1.) Di setiap baris, angka pertama selain 0 harus 1 (leading 1). [[Berkas:]]
2.) Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.
3.) Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan dari leading 1 di atasnya.
4.) Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebut Eselon-baris tereduksi
Contoh: syarat 1: baris pertama disebut dengan leading 1
\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & -5 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & -8 & 8\\ \end{bmatrix}
syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2
\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & -5 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & 0 & 0\\ \end{bmatrix}
syarat 3: baris pertama dan ke-2 memenuhi syarat 3
\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & 1 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & 0 & 0\\ \end{bmatrix}
syarat 4: matriks dibawah ini memenuhi syarat ke 4 dan disebut Eselon-baris tereduksi
\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 2 & 5\\ 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 6\\ \end{bmatrix}

Operasi Dalam Matriks

Dua buah matriks dikatakan sama apabila matriks-matriks tersebut mempunyai ordo yang sama dan setiap elemen yang seletak sama.
Jika A dan B adalah matriks yang mempunyai ordo sama, maka penjumlahan dari A + B adalah matriks hasil dari penjumlahan elemen A dan B yang seletak. Begitu pula dengan hasil selisihnya. Matriks yang mempunyai ordo berbeda tidak dapat dijumlahkan atau dikurangkan.
Jumlah dari k buah matriks A adalah suatu matriks yang berordo sama dengan A dan besar tiap elemennya adalah k kali elemen A yang seletak. Didefinisikan: Jika k sebarang skalar maka kA = A k adalah matriks yang diperoleh dari A dengan cara mengalikan setiap elemennya dengan k. Negatif dari A atau -A adalah matriks yang diperoleh dari A dengan cara mengalikan semua elemennya dengan -1. Untuk setiap A berlaku A + (-A) = 0. Hukum yang berlaku dalam penjumlahan dan pengurangan matriks :
a.) A + B = B + A
b.) A + ( B + C ) = ( A + B ) + C
c.) k ( A + B ) = kA + kB = ( A + B ) k , k = skalar
Hasil kali matriks A yang ber-ordo m x p dengan matriks B yang berordo p x n dapat dituliskan sebagi matriks C = [ cij ] berordo m x n dimana cij = ai1 b1j + ai2 b2j + ... + aip bpj

[sunting] Matriks Balikan (Invers)

JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau invers dari A dan dapat dituliskan B = A − 1 ( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan A = B − 1. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.
Matriks A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} dapat di-invers apabila ad - bc ≠ 0
Dengan Rumus =
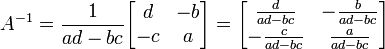
A^{-1} = \frac{1} {ad-bc}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} = \begin{bmatrix} \frac{d} {ad-bc} & -\frac{b} {ad-bc} \\ -\frac{c} {ad-bc} & \frac{a} {ad-bc} \\ \end{bmatrix}
Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-invers dan (AB) − 1 = B − 1A − 1

Contoh 1:
Matriks
A = \begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix} dan B = \begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}
AB = \begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix}\begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = I (matriks identitas)
BA = \begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = I (matriks identitas)
Maka dapat dituliskan bahwa B = A − 1 (B Merupakan invers dari A)

Contoh 2:
Matriks
A = \begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix} dan B = \begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}
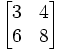
AB = \begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 3 & 4 \\ 6 & 8 \\ \end{bmatrix}
BA = \begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 17 & 21 \\ 15 & 19 \\ \end{bmatrix}
Karena AB ≠ BA ≠ I maka matriks A dan matriks B disebut matriks tunggal.

Contoh 3:
Matriks
A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \\ \end{bmatrix}
Tentukan Nilai dari A-1
Jawab:
A^{-1} =\frac{1} {(3)(2)-(5)(1)}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {6-5}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {1}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix}

Contoh 4:
Matriks
A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \\ \end{bmatrix}, B = \begin{bmatrix} 3 & 2 \\ 2 & 2 \\ \end{bmatrix}, AB = \begin{bmatrix} 7 & 6 \\ 9 & 8 \\ \end{bmatrix}
Dengan menggunakan rumus, maka didapatkan
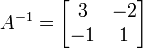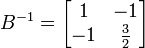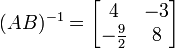
A^{-1} = \begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix}, B^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}, (AB)^{-1} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}
Maka
B^{-1} A^{-1}= \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}\begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}
Ini membuktikan bahwa (AB) − 1 = B − 1A − 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Diposting oleh di

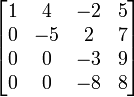
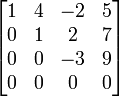
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)